포스팅 개요
이번 포스팅은 딥러닝 기반 추천 시스템에서 유명한 논문인 neural collaborative filtering에 대한 paper review입니다. 일명 ncf라고 불리우는 neural collaborative filtering 논문은 추천 시스템 논문 중 collaborative filtering 방법인 matrix factorization 방법을 개선한 논문입니다. 해당 논문을 간단하게 정리하고 요약하려고 합니다.
논문은 아래 링크에서 볼 수 있습니다.
포스팅 본문

neural collaborative filtering paper의 핵심 요약
먼저, neural collaborative filtering 논문을 간단하게 요약하자면 아래와 같습니다.
- implicit feedback data 활용
- 기존 Collaborative Filtering model(Matrix Factorization)을 단점을 지적하며 개선할 수 있는 방향 제시
- Deep Neural Network(Deep learning) 방법을 사용해 linear하지 않은 Matrix Factorization 방법을 non-linear하게 개선
- 이를통해 feature representation을 더 풍부하게 함
- Matrix Factorization은 neural collaborative filtering(NCF)의 일반화 버전임
- MLP 구조는 user-item interaction 표현을 neural net에 넣는 구조
- NCF는 MLP + GMF 구조임
Abstract
neural collaborative filtering paper의 abstract에서는 아래와 같은 내용을 소개해주고 있습니다.
- Collaborative Filtering 문제를 해결하고자 함
- Implicit feedback에 기반하여 recommender system 문제인 Collaborative Filtering를 다룸
- 이떄 Neural networks를 기반으로 해서 기술을 개발하려고 노력
- 과거에도 Deep learning for recommendation 방법이 존재함
- 하지만, text나 acoustic feature of music과 같이 보조 information 용도로 사용
- 결국 latent features of users and items를 위해 Matrix Factorization에 계속 의존함
- 본 논문에선 Neural Collaborative Filtering을 제안함
- 일반적이고 framework안에서 MF를 일반화 할 수 있음
- user-item interaction function을 학습하기 위해 multi layer perceptron을 제안
Introduction
본 논문에서의 소개 부분입니다. introduction에는 아래와 같은 내용을 담고 있습니다.
- Matrix Factorization은 가장 인기가 많은 추천 방법이 되었음
- user와 item의 latent feature vector를 사용
- netflix prize 이후 MF는 사실상의 추천 모델의 접근 방법이 되었고 많은 후속 연구들도 MF 방법으로 많이 나옴
- 그러나 Matrix Factorization 추천 방법은 한계가 존재함
- sample choice of the interaction function으로 성능에 지장이 있음
- 단순 inner product는 multipliaction of latent feature를 linear하게 결합함
- sample choice of the interaction function으로 성능에 지장이 있음
- 따라서 본 논문에서는 deep neural network(deep learning)를 interaction function from data를 배우기 위해 사용
- 기존 문헌에서는 딥러닝 방법으로 추천 시스템을 활용하는 것이 많지 않았음
- 딥러닝 구조를 추천 시스템에 사용한다고 해도 text 설명이나, audio feature, image 등에서 보조 정보를 모델링 하는데 사용됌
- 결국 user와 item latent feature를 겹합하는데에는 Matrix Factorization을 사용함
- 본 논문에서는 위 문제들을 해결하려고 함
- implict feedback 데이터에 focus를 둠
- Deep Neural Network를 이용해 노이즈가 많은 implicit feedback signal을 모델링 하는 방법에 대한 탐구
Preliminaries
본 논문에서는 본격적인 내용에 들어가기 앞서 여러가지 배경설명을 먼저 해주고 있습니다. 본 파트는 그러한 내용을 담고 있습니다.
neural collaborative filtering에 대한 배경 설명은 아래와 같습니다.
learning from implict data
user u와 item i의 interaction이 있을 경우label을 1로 설정합니다. 여기서 interaction은 video를 시청했거나 구매했거나 등의 implicit data입니다. 만약, interaction이 없으면 0으로 설정합니다.
여기서 주의할 점이 있습니다!
- user u가 item i를 좋아한다는 것을 의미하지 않습니다.
- 0에서도 마찬가지 논리임
- interaction이 없는 것이지 비선호 한다는 의미가 아님!
user의 선호를 분명하게 할 수는 없다고 본 paper에서는 설명하고 있습니다. 왜냐하면 user가 item을 좋아할 수도 있지만, 해당 item을 모르는 경우에도 Yu,i = 0이 되기 때문입니다. 따라서 관찰되지 않은 항목의 점수를 측정하는 문제로 공식화 할 수 있다고 본 논문에선 주장하고 있습니다.

- 수학 기호
- y ̂(u,i)=f(u, i |θ) 을 학습
- y ̂(u,i) : predict score of interaction y(u,i)
- θ : model parameter
- ƒ : function
θ를 학습시키기 위한 방법은 Pointwise learning, Pairwise learning 2가지가 존재한다고 합니다.
- pointwise learning은 regression 문제에 활용되고 target y와 predict(y ̂(u,i)) 차이를 최소화
- pairwise learning은 observed entries should be ranked higher than the unobserved ones 되어야 함
- Pointwise와 같이 y ̂(u,i)와 y의 차이를 최소화 하는 것과 다르게 observed된 y ̂(u,i)와 unobsered y ̂(u,i)의 margin을 최대화
본 논문에서 제안하는 Neural Collborative Filtering(NCF)는 y ̂(u,i)를 측정할 때 neural network를 사용하므로 자연스럽게 pointwise와 pairwise를 둘 다 사용한다고 합니다.
Matrix Factorization
- p_u : latent vector for user u
- q_i : latent vector for item i
MF는 estimates an interaction y_(u,i)를 하기 위해 p_u 와 q_i를 inner product합니다. 그 중 K는 latent space의 차원입니다. Matrix Factorization 추천 시스템 방법의 특징은 아래와 같습니다.
- User latent factor와 item latent factor의 양방향 interaction을 모델링
- 각각이 독립적이고 같은 가중치로 선형 결합
- Latent factor의 linear model로 여겨짐

추천 시스템에서 Matrix Factorization(MF) 방법의 한계
본 논문에서는 추천 시스템에서의 Matrix Factorization 방법의 한계를 지적합니다. Matrix Factorization은 User와 item을 같은 latent space에 매핑하고 inner product 등으로 유사도를 구하는 방법을 취합니다. 아래 그림으로 MF의 한계점을 설명하는데요.

그림 (a)에서 보면 사용자끼리의 유사도는 S_23 (0.66) > S_12 (0.5) > S_13 (0.4)가 됩니다. 즉, user2,3이 가장 가까운 셈이죠. 이를 기하학적으로 표현하면 그림 (b)의 실선과 같습니다. 여기서 새로운 user 4가 들어왔다고 가정해보죠. user4는 (a) 표의 입장에서 S_41 (0.6) > S_43 (0.4) > S_42 (0.2)순으로 유사도가 크게 나오는 것을 볼 수 있습니다. 그러나 이를 기하학적으로 표현하면? 표현할 수 없게 되는 것입니다.
- 4와 1을 가장 가깝게 하면 P4가 P3보다 P2에 가깝게 됌
이러한 현상은 ranking loss가 커지는 것을 초래한다고 합니다. 즉, 추천 시스템에서 Matrix Factorization을 적용할 때의 한계를 보여주는 점입니다. 단순한 fixed inner product를 사용하면 복잡한 user-item의 interaction을 저차원 latent space에서 측정할 때 문제가 발생된다고 하네요.
Neural Collaborative Filtering
이제 본격적으로 본 논문에서 주장하는 Neural Collaborative Filtering 추천 시스템 방법에 대해 설명합니다. 위에서 MF의 단점과 그에 따른 본 논문에서 진행하고자 하는 방향에 대해 대략적으로 설명해주었는데요. 이제 이 내용을 상세하게 다뤄줍니다.
General Framework
여기서 주장하는 General Framework는 Collaborative Filtering(CF)의 full neural 처리를 허용하기 위해서 multi-layer representation을 활용 한다고 합니다.

본 논문은 순수한 Colaborative Filtering setting에 focus를 두기 위해 user, item의 ID만 one-hot encoding 형태의 입력으로 넣는다고 합니다. 이렇게 획득된 user(item) embedding은 latent vector라고 볼 수 있습니다. 즉, 아래 그림과 같이 말이죠.
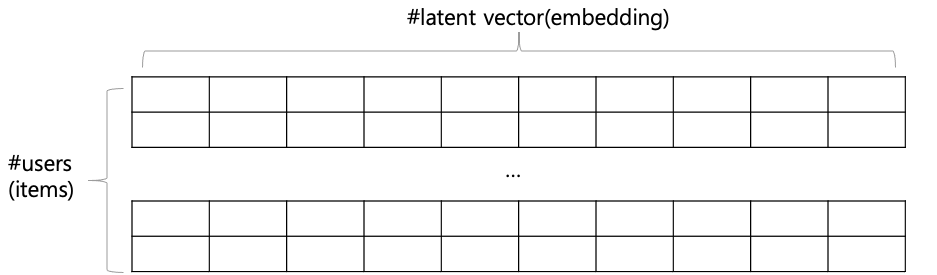
이 구조에서 User, item embedding은 Multi-layer neural architecture에 넣어줍니다. 그리고 이를 Neural collaborative filtering layers라고 본 논문에서 칭합니다. 또한, Final output layer는 predict score y ̂(u,i) 해서 구해줍니다. 이때 Pointwise를 사용해서 y ̂_(u,i)와 y_(u,i)를 최소화합니다. BPR과 같은 pairwise는 향후 연구로 둔다고 하네요.
각종 수식과 본 논문에서 주장하는 내용은 아래 사진과 같습니다.

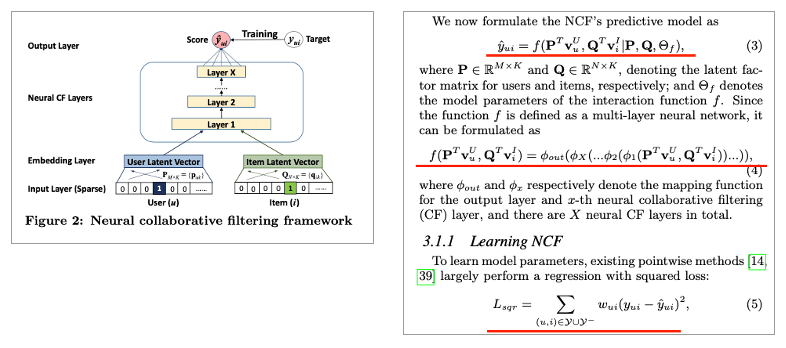
또한, 본 논문에서는 아래와 같은 수식을 보여주면서 General Framework를 설명하고 있는데요.

여기서 y_(u,i)는
- 1 : item i는 u와 관련성이 있다. 아니면 0
y ̂_(u,i)는
- •Predict score y ̂_(u,i)는 i가 u와 얼마나 관련 있는지로 표현
이를 [0, 1] 범위로 제한한다고 합니다. 이렇게 하면 확률 함수로 쉽게 사용 가능 (ø_out 에서)하기 때문이죠. 0, 1로 지정했으니 식 (6)과 같은 형태로 likelihood function을 정의할 수 있습니다. 약간 베르누이 분포와 비슷헌 구조입니다. (사실상 베르누이 분포인듯?) Object function은 (7)과 같은 식입니다. 뭔가 익숙하다? 라는 느낌을 받으시는 분들도 있으시겠지만, Binary cross-entropy loss와 같은 구조입니다. 또한, Negative instance Y- 를 위해 균일하게 샘플링 한다고 합니다.
Generalized Matrix Factorization
이제 Generalized Matrix Factorization을 설명합니다. 줄여서 GMF라고 논문에서 소개하고 있습니다. Matrix Factorization은 Neural Collaborative Filtering의 speci

al case 형태라고 본 논문에서 주장하고 있습니다.

이때 수식이 아래와 같으면 MF 형태라고 합니다.
- •a_out : identity function
- h : [1, … , 1]_1xk
또한, 수식이 아래와 같을 때는 GMF(MF를 일반화한 모델)라고 합니다.
- a_out : sigmoid function
- h :[h1, …hk]_1xk uniform 하지 않음
Multi-Layer perceptron
또한, 단순 MF구조가 아닌 멀티 레이어 퍼셉스론 구조(Multi layer perceptron)를 활용하기도 합니다. 단순 vector를 concatenation하는 것은 user와 item latent features사이에 interaction을 간주하지 않기 때문이죠. 죽, 이는 Collaboratvie Filtering 효과를 모델링 하기에 부족합니다. 그래서 MLP라는 구조를 하나 더 제안합니다. User와 item의 latent features의 interaction을 배우기 위함입니다. 이렇게 하면
- Only a fixed element0wise product하는 GMF와 다르게 많은 수준의 flexibility와 non-linearity를 제공할 수 있음
- Tower 구조

NeuMF ( Fusion of GMF and MLP )
이제 본 논문에서 주장하는 최종 모델을 소개합니다. 그 모델은 앞서 소개한 Generalized Matrix Factorization(GMF)와 Multi-layer perceptron(MLP)를 합친 NeuMF 구조입니다.
- GMF : latent feature interaction을 위해 linear kernel을 도입
- MLP : data에서 interaction을 배우기 위해 non-linear kernel 도입
이 둘을 fuse한 방법입니다. Same embedding layer로 share하는 방법이 존재하기도 한다고 하네요. 하지만, 이 방법은 성능의 한계가 있을 수도 있다고 합니다. 왜냐하면 동등한 embedding size를 가져야 하기 때문입니다. 만약, 두 모델의 최적의 embedding 크기가 많이 변화하는 dataset의 경우 최적의 앙상블(ensemble) 효과를 얻지 못할 수도 있다고 합니다. 그래서 GMF, MLP를 별도의 embedding으로 학습 후 last hidden layer concating하는 구조를 취합니다.

또한, 본 논문에서는 Pre-trained된 구조를 사용한다고 합니다. 이는 딥러닝(Deep learning)에서 convergence와 performance를 위해 initialization하는 것은 매우 중요하기 떄문에 (실제로도 그렇구요) 사용한다고 합니다. NeuMF에서는 GMP와 MLP의 pre-trained된 model로 initialize하는 것을 제안합니다,
- GMP와 MLP를 random initialization으로 convergence할 때까지 training
- 훈련된 모델의 파라미터를 NeuMF에서 활용
- 알파 값을 이용해 가중치를 부여 (코드 상에서는 0.5씩)

Experiments
이제 실험입니다. 모델 성능 평가를 위해서 아래와 같이 3가지 관점으로 실험을 진행한다고 합니다. 그래서 각각 RQ1, RQ2, RQ3에 대해서 평가 설명이 이루어지고 있습니다.
- Outperform state-of-the-art가 나왔는가? (RQ1)
- Log loss와 Negative Sampling의 효과 (RQ2)
- Layer가 더 깊어지면 user-item interaction을 배울 때 도움이 되는가? (RQ3)
Performance Comparison(RQ1)
eALS, BPR과 비교해 State-of-the-art를 달성했다고 합니다. 특히, Pinterest의 경우 적은 predictive factor (8개)를 했는데도 eALS, BPR의 large factor(64)보다 좋게 나온 것을 확인할 수 있습니다. 이떄, MLP의 경우 hidden layer를 더 쌓을 수록 성능이 좋아지고 이는 뒷 부분에 추가로 설명됩니다. 일단, 여기서는 단순히 3개를 기준으로 보여줍니다.
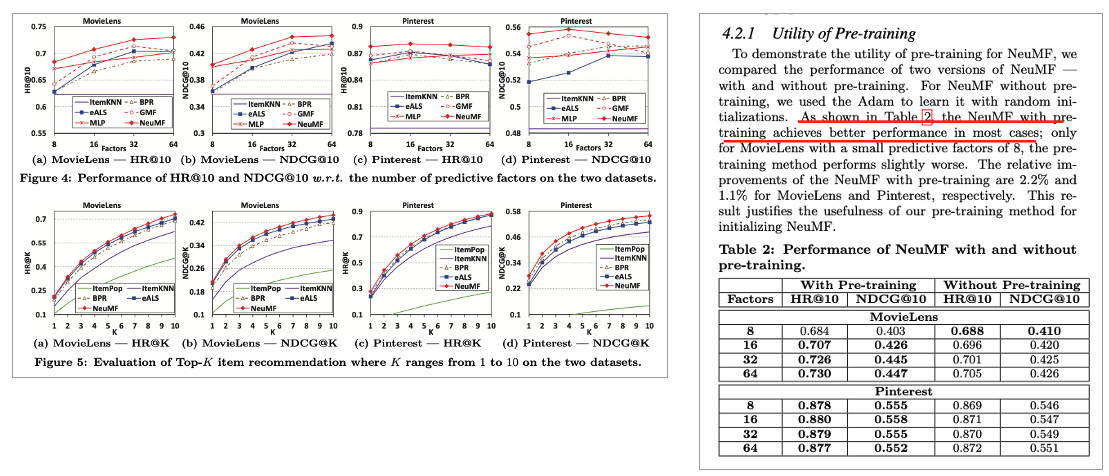
Log Loss with Negative Sampling(RQ2)
여기서는 아래 3가지의 소주제로 간단하게 성능과 평가를 확인할 수 있습니다.
1. More iteration을 하면 NCF model의 training loss는 감소하고 성능은 내려감
Most effective는 처음 10 iteration때입니다. 그 이상은 overfitting 경향이 보이고 있습니다. 실제 아래 사진을 보면 그러하죠.
2. NeuMF, MLP, GMF를 비교했을 때
NeuMF가 가장 적은 training loss를 달성합니다. 즉, 가장 좋은 성능을 보여주죠. 그리고 나서 MLP > GMF 순으로 성능이 나옵니다.
3. Negative Sampling
Negative Sampling을 Different negative sampling ratio를 두고 실험을 진행했습니다. 단순히 sampling을 1개로 했을 때 보다 다수의 negative sampling이 더 benefical하는 것을 볼 수 있습니다.
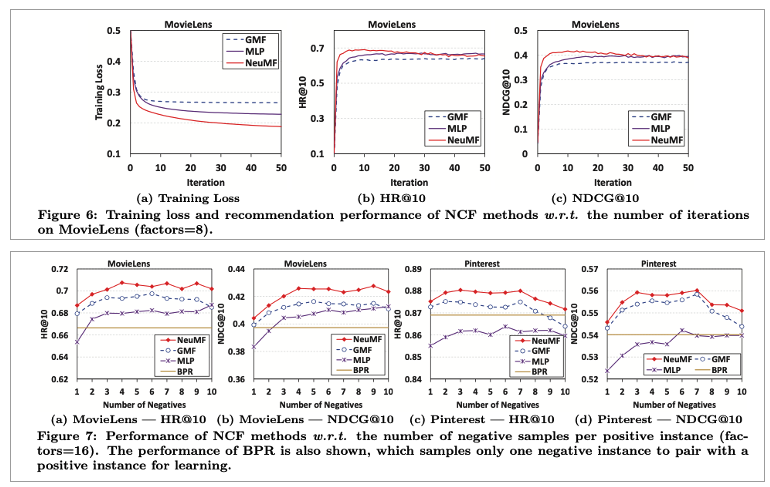
Is Deep Learning Helpful(RQ3)
이 부분에서는 딥러닝 구조(Deep network 구조)가 추천 시스템 테스크에서 (recommendation task)에서 유리한가?에 대한 실험입니다. 여기서는 MLP를 hidden layer를 다르게 해서 조사합니다. 결론은 더 많은 layer를 stack할 수록 좋습니다.

마무리
본 포스팅에서는 Matrix Factorization 기반의 추천 시스템을 딥러닝(Deep network)구조를 사용해서 개선하는 방법을 보여줍니다. 다른 feature를 넣지 않고 단순히 item, user id만 넣어 기존 MF 방식을 따르지만, non-linear한 구조를 따르게해서 성능 향상을 보여준 논문입니다. 다음 포스팅에서는 해당 논문에 대한 코드를 tensorflow2 버전의 keras를 사용해서 코드를 수정하고 설명하도록 하겠습니다.




