포스팅 개요
이번 포스팅은 추천 시스템 논문 리뷰 포스팅입니다. 본 논문의 제목은 Hierarchical attention and feature projection for click-through rate prediction(CTR prediction)이라는 논문입니다.
본 논문은 추천 시스템 모델을 활용해 클릭률(CTR)을 향상 시킬 수 있는 방법을 소개하는데요. Hierarchical 구조를 활용해 feature 사이의 중요도를 추출하고 low-order 그리고 high-order feature interaction을 모델링하는 방법을 소개합니다.
본 포스팅에서 리뷰한 논문 링크는 아래와 같습니다.
포스팅 본문

본 포스팅은 추천 시스템 논문인 Hierarchical attention and feature projection for click-through rate prediction(CTR prediction) 논문을 리뷰한 포스팅입니다. 본 논문에서 주장하는 추천 시스템은 feature의 중요성을 강조하는 논문입니다. 기존에 추천 시스템 방법론들(클릭률 예측 방법들)은 각 feature의 중요성을 무시하거나 feature learning을 동등하게(equally) 진행했다는 것을 지적하면서 본 논문에서는 HAFP(Hierarchical Attention and Feature Projection Neural Network)을 제안합니다. 이때, 계층 어텐션 구조(Hierarchical attention)을 사용해 dominant 그리고 generalized feature들과 feature interaction을 jointly하게 추출하도록 제안합니다. 이를 위해서 Salient feature encoder, Meaningful second-order interaction encoder, Dominant high-order interaction encoder의 encoder들을 도입해 모델링을 수행합니다.
Introduction
본 논문에서 주장하는 CTR prediction의 Key challenge는 model feature engineering을 얼마나 효율적으로 하는가?라고 합니다. 이를 위해 전통적으로는 LR(Logistic Regression), Factorization Machine(FM) 등과 같은 방법을 사용했었죠. 이러한 연구들을 통해서 low order(first order and second order)와 high order feature interaction이 중요하다는 것을 검증했었습니다.
그러나, 기존 방법들은 low order 및 high order feature interaction 정보를 jointly하게 포착하지 않았다고 본 연구에서는 말하고 있습니다. 그렇기에
- 서로 다른 feature들은 다른 importance를 가져야합니다. 예를 들어 occupation은 사용자의 income을 예측할 때 age보다 중요하니까요.
- 모든 pair-wise feature interaction이 equally하게 사용되면 안된다고 합니다. 예를 들어 사용자의 income을 예측할 때 occupation과 home address 조합이 age와 gender interaction 보다 좋을태니까요.
- high order feature interaction은 매우 크고 무거운 연산이 필요합니다. 또한, 서로 다른 layer feature interaction은 feature learning을 위한 서로 다른 semanctic information을 담고 있으므로 덜 유용한(less uesful) interaction은 기여도가 제한적이기 때문에 lower weight를 할당해야 계산을 줄일 수 있습니다.
- 클릭률 예측(CTR predction) task는 sprarse하고 categorical합니다. 기존 방법들은 second order feature interaction을 위해 inner product 등을 사용했는데 이는 너무 간단하기에 feature learning을 제한하고 그 효과로 성능 손상이 일어납니다.
본 논문은 이러한 것들을 해결하고 다루기 위해 Hierarchical Attention and Feature Projection neural network(HAFP)를 제안합니다. HAFP는 다음과 같은 특징으로 정리될 수 있습니다.
- 서로 다른 feature의 중요성이 task에 대해 다르기 때문에 salient feature를 global-local context module을 활용해서 관련 기능을 검색하게 합니다.
- second-order feature interaction에 weighted score를 매겨 계산합니다.
- 각 layer의 high order feature interaction을 선택적으로 집계(aggregated)하여 의미있고 유익한 feature representation을 학습할 수 있습니다.
- second order feature interaction의 품질이 high order feature interaction에 영향을 미치기 때문에 bilinear function을 고안하여 세분화된(fine-grained) feature interaction을 학습하도록 합니다.
요약하자면 본 논문에서 말하고자 하는 바는 아래와 같습니다.
- 제안한 방법은 feature learning에 필요한 relevant contexts를 충분히 활용할 수 있습니다.
- 기존에 연구된 bilinear-interaction layer에서 영감을 받아 projective bilinear function을 도입해 inner product을 사용해 co-projection matrix를 생성하고 Hadamard product를 사용해 interation embedding을 생성했습니다.
- Attentive global-local context module은 의미 있는 feature를 적응적(adaptivly)으로 선택하도록 설계하였습니다. 이는 globally 분포를 나타내는 공통 정보를 강조하는 동시에 locally하게 나타나는 특징화(characterized) 된 정보도 강조할 수 있습니다.
- 다양한 실험 결과, 성능 향상이 나왔습니다
Related work
본 논문에서 related work으로 소개한 연구들을 간단하게만 정리해보겠습니다. 자세한 것은 논문을 참고해주세요.
1. Traditional methods
전통적인 추천 시스템, 클릭률 예측 연구에서는 Factorization Machine과 FM을 연장한 연구들 Field-aware Factorization Machine(FFM), Attentional Factorization Machine(AFM)등이 있습니다.
2. Deep learning based methods
딥러닝 기반 추천 시스템, 클릭률 예측 연구에서는 FNN, PNN(Product-based neural network), Wide and Deep learning(Wide & Deep), DeepFM, Deep&Cross 등이 있습니다. 또한, 어텐션(attention) 매커니즘을 활용한 방법도 있는데요. Interpretable Hierarchicla Attention Mechanism(InterHAt)도 있고 ACN, HoAFM 등의 연구도 있다고 언급하고 있습니다.
Related work는 여기까지 정리해두겠습니다. 자세한 것은 논문을 참고해주세요!
Proposed algorithm

본 논문에서 주장하는 클릭률 예측 모델인 HAFP 전체 프레임워크는 위 그림과 같습니다. 눈에 띄는 부분은 노란색으로 칠해진 Feature Learning Layer인데요. 이 layer에 속한 3개의 encoder가 이 논문에서 주장하는 클릭률 예측 모델의 핵심입니다.
그러면 각 Encoder를 자세히 살펴보겠습니다.
Salient feature encoder
가장 먼저 소개드릴 핵심 인코더는 본 논문에서 Salient feature encoder라고 칭하고 있는 인코더입니다. 본 인코더는 아래 그림과 같은 모듈 형태로 구성되어 있는데요. Salient feature encoder의 핵심은 global gate와 local gate이겠구나! 라고 눈에 띄실겁니다. 본 논문에서 이를 attentive global-local contexts module이라고 칭하고 있습니다.

Global Gate(global context module)쪽은 다음과 같은 순서대로 데이터를 입력 받습니다.
- 필드의 임베딩 벡터 E를 가져옵니다
- 각 임베딩에 mean pooling을 적용해 global information를 구합니다( 수식 1 ). 이렇게 나온 global weight vector를 A로 지정합니다.
- 이후 neural network 구조 형태로 global weight에 따라 각 feature embedding의 weight를 학습합니다(수식 2). 이렇게 생성된 G를 global gate라 칭합니다.
- 3번에서 구한 weight와 embedding을 계산하여 reweight합니다 (수식 3).
이렇게 global gate를 계산하여 임베딩의 글로벌 어텐션 정보를 학습하게 되는데요. 위에서 언급드린 수식들은 아래 사진과 같습니다.

global gate를 계산할 뿐만 아니라, 각 feature의 특징 정보(characterized information)을 포착하기 위해서는 local context도 고려해야 한다고 본 논문에선 주장하고 있습니다.
따라서, 비슷한 방법으로 local context를 계산하게 되는데요. 그 순서를 정리하면 아래와 같습니다.
- 임베딩 벡터를 가져옵니다.
- 임베딩 벡터에 direct로 nerual network 구조를 적용합니다(수식 4). 이렇게 생성된 벡터를 L이라고 칭하며, local gate라고 칭합니다.
- local weight와 embedding을 연산해 V을 구합니다(V_l)(수식 5).
위 과정을 수식으로 표현하면 아래 그림의 식 4, 식 5(식4 아래에 있는 식)입니다. local gate에서의 특징은 input field embedding vector와 동일한 shape를 가진 것이라고 하네요.
이렇게 구해진 local gate의 값과 global gate의 값을 활용해 salient feature vector를 구하게 됩니다. 각 방법에 따라 element-wise multiplication(곱하기 모양) 또는 addition(더하기 모양) 연산을 취하게 됩니다. ( 식 6 )

본 논문에서는 이 과정을 통해 global 정보와 local 정보를 포괄적으로 강조할 수 있다고 합니다. 따라서, 각 feature의 weight들은 contribution에 따라 동적으로 조정될 수 있다고 하네요.
Meaningful second-order interaction encoder
본 논문에서 소개하는 중요한 encoder 중 하나는 meaningful second order interaction encoder입니다. 이 인코더는 2차 상호 작용(second order feature interaction)을 효과적이고 정확하게 모델링 할 수 있다고 합니다.
기존 방법에는 inner product와 Hadamard product가 일반적으로 많이 사용되었지만, 이들은 너무 간단해서 sparse dataset에서 feature interaction을 효과적으로 계산하기엔 부족하다고 하네요. 이를 보완하기 위해 이전에는 FiBiNET이라는 연구가 있었는데, 이것도 pair-wise를 완전히 고려하지 않는다고 합니다.
따라서, 본 논문의 저자들은 더 세분화 된 bilinear function을 도입해 전체 매핑 관계를 취할 수 있고 inner product와 hadamard product의 장점을 가지고옵니다. 해당 인코더는 아래 사진과 같은 구조를 가지고 있습니다.

Meaningful second order interaction encoder는 크게 p와 q로 나뉘어집니다.
P를 구하는 과정은 다음과 같습니다.
- 앞서 구한 salient feature encoder의 결과인 V를 가지고 옵니다.
- i와 j는 i1 <= i <= m 그리고 i < j <=m 관계를 가지고 있습니다.
- inner product를 통해 i와 j사이의 feature들의 second order feature interaction을 수행합니다(식 7)
- 일반적으로 모든 feature interaction이 final task에 전부 연관되어 있지 않습니다. 연관성 없는 feautre는 오히려 noise하고 모델의 일반화 성능을 악화시킬 수 있는데요. 이를 방지하기 위해 attention score를 MLP 구조를 활용해 계산해줍니다.( 식 8, 9 )
P를 구하는 수식은 아래 사진과 같습니다.

p를 구하였음에도 q를 또 다시 구하는 이유는 일종의 residual connection의 효과를 보기 위함입니다. residual network는 vanishing gradient(기울기 손실) 문제를 완화해주고 deep feature를 더 포괄적으로 다뤄주기 때문입니다.
따라서 아래와 같은 순서로 q를 구하게 되는데요. p와는 다른 정보를 사용합니다.
- embedding vector를 가져옵니다.
- inner product를 통해 second order feature interaction을 수행합니다(식 10).
- attention score를 구하고(식 11) 이를 식 10에서 구한 값에 곱해줍니다.
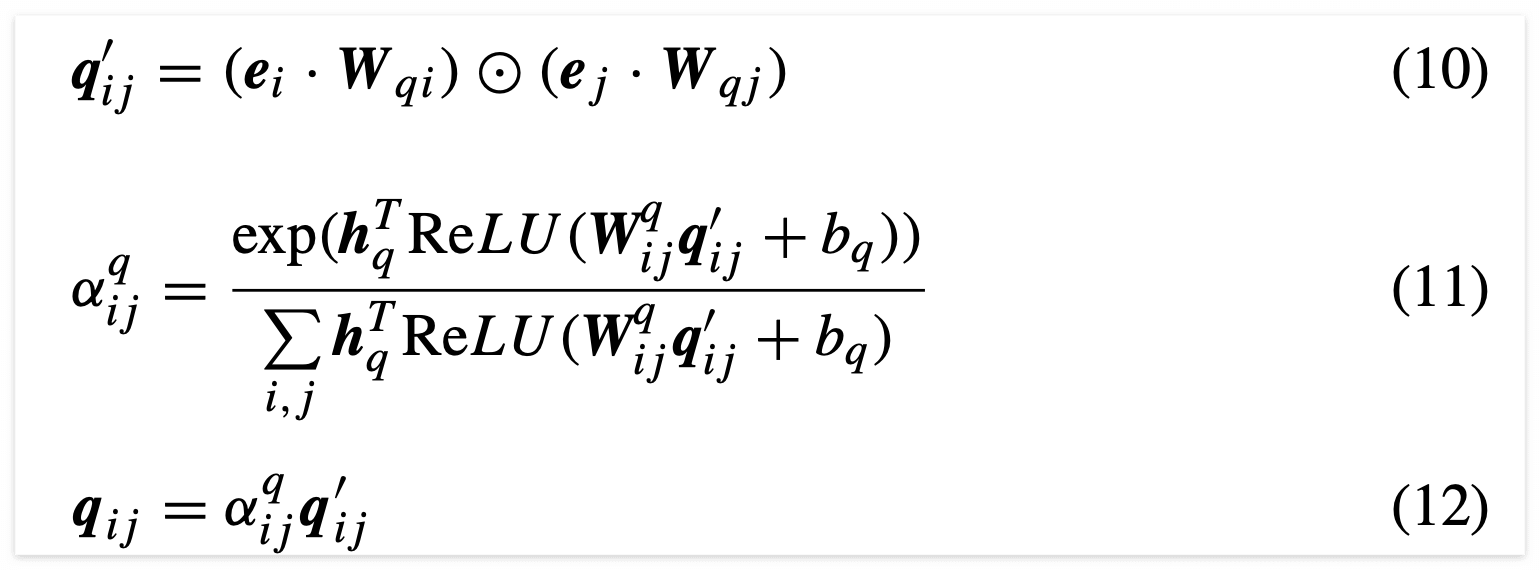
이 과정을 통해 second order feature interaction 과정을 좀 더 풍부하게 다뤄주게 됩니다. 본 인코더의 마지막으로 모든 요소를 전부 concatenation한 후 Fully-connected layer를 통해 포괄적인 second order feature interaction을 학습합니다(식 13). 이 결과로 풍부한 정보를 부여할 수 있게 되는것이죠.

Dominant high-order interaction encoder
일반적으로 high order feature interaction을 위해서 deep learning network 구조를 많이 활용합니다. 여기서 말하는 deep learning network는 fully connected network 구조입니다. 또한, 계층적(hierarchical) 구조의 장점을 활용해서 효율적이고 표현력이 좋은 구조를 구성하게 됩니다.
하지만, 일반적인 방법은 layer 사이의 관계를 무시하는 경향이 있다고 본 논문에서 이야기하고 있습니다. 직관적으로 봤을 때 서로 다른 layer에서 나오는 feature들은 서로 다른 정보를 담고 있겠죠? 따라서 본 논문에서는 어텐션 매커니즘을 활용해 지배적인 것과 관련성 없는 것들을 선택할 수 있도록 동적으로 가중치 하는 구조를 구성해 feature extraction 성능을 향상시킨다고 합니다. 본 논문에서 제안한 구조는 아래와 같습니다.

본 구조의 순서는 다음과 같이 진행됩니다.
- 포괄적으로 정보를 담은 second order feature interaction 값을 feed forward neural network 구조로 넣어줍니다 (식 14). 이때 H0는 hs로써 second order feature interaction 값입니다.
- layer를 거치면서 각각의 output을 계산하게 됩니다(식 15).
- layer마다 제공하는 서로 다른 정보들이 있을 수 있습니다. 예를 들어, 0번째 layer와 비교 했을 때 최상단 layer는 좀 더 포괄적인 정보를 담고 있겠죠? 따라서, 좀 더 세부적이고 유용한 정보를 구성하기 위해 attention mechanism을 활용해서 attention score를 구하고(식 16) 이를 layer output에 곱해줍니다(식 17).
위 과정을 담은 수식은 아래와 같습니다.
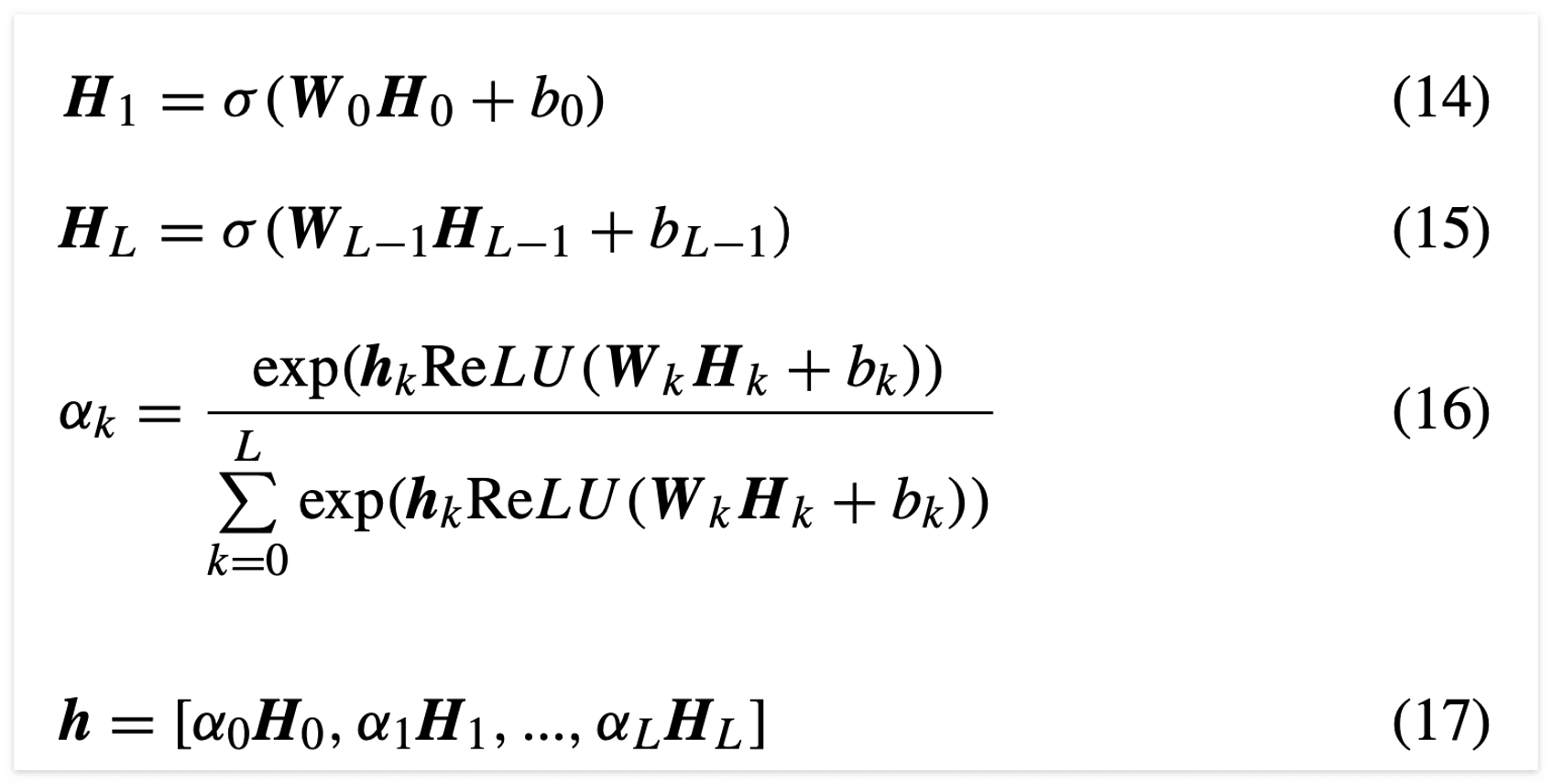
이와 같이 계층적 feature는 feature learning을 위해서 동등하지 않게(not equally) 집계될 수 있습니다.
이렇게 논문에서 제안한 핵심 요소 인코더들을 다 알아봤습니다.
Prediction layer
CTR 예측을 푸는 본 논문의 구조이므로 인코더의 마지막 아웃풋을 활용해서 weight를 곱하여 최종 예측을 수행합니다(식 18). 그리고 이때 loss는 크로스 엔트로피(cross entropy) loss를 사용해서 학습한다고 하네요(식 19).

Experiements and analysis
본 논문에서 주장한 모델 HAFP가 얼마나 좋은 성능 향상을 띄는지 이제 실험적으로 비교합니다. 실험 내용은 본 포스팅에선 간단하게만 다루겠습니다. 궁금하신 분들은 논문을 보셔서 자세히 참고하시길 바랍니다.
Dataset & Evaluation metrics
본 논문에서 활용한 데이터 셋은 Criteo와 Avazu 데이터 셋입니다. 두 데이터 셋 모두 클릭률 예측 문제에서 많이 활용되는 데이터 셋입니다. 그리고 활용한 메트릭은 Area Under Curve(AUC)와 Logloss를 사용해 평가를 진행했습니다.
Baseline models
본 논문에서 제안한 모델과 비교하는 다른 베이스라인 모델들은 LR, FM, AFM, NFM, DeepFM, InterHAt, FiBiNET입니다. 총 7개의 모델과 비교했으며 HAFP의 성능이 기존 모델들보다 뛰어나다는 것을 실험적으로 보여줍니다.
Experiments Result
본 포스팅에서는 실험 결과 중 2가지만 요약해 정리해서 보여드리겠습니다. 하나는 AUC, Logloss 성능 비교이고 하나는 HAFP의 encoder를 다르게 변화주었을 때의 성능 변화를 측정한 것입니다.
가장 먼저, AUC, Logloss 성능 비교입니다. Logloss는 낮으면 낮을 수록 좋은 것이고(loss 이기 때문에) AUC는 높을수록 좋은 것입니다. 어쩌면 당연하게도(?) 본 논문에서 제안하는 방법이 가장 좋은 성능을 보여주고 있습니다.

두 번째 실험 비교는 본 논문에서 제안한 HAFP 모델에서 인코더를 다르게 변환했을 때 어떤 성능이 나오는지 살펴본 결과입니다. 이 실험을 진행한 이유는 hierarchical attention mechanism의 영향을 살펴보기 위함인데요. 이를 위해서 HAFP의 변형 모델을 아래와 같이 구성하였습니다.
- FP-0 : HAFP에서 salient feature encoder와 meaningful second-order interaction encoder 그리고 dominant high-order interaction encoder에서 어텐션 메커니즘을 빼버린 모델입니다.
- FP-1 : HAFP의 meaningful second order interaction encoder와 dominant high order interaction encoder에서 attention mechnism을 제외한 모델입니다.
- FP-12 : HAFP의 dominant high order interaction encoder에서만 attention mechnism을 제외한 모델입니다.
이들 각각의 성능을 비교한 표는 다음 사진에 나오는 table3와 같은데요.

이 표에 대한 내용을 요약하자면 다음과 같습니다.
- FP-0는 다양한 HAFP 변형 모델들 중 가장 성능이 안 좋습니다. 그럼에도 FiBiNET와 비슷한 구조를 가졌는데 FiBiNET보다는 좋은 성능이 나왔다고 하네요. FP-0와 FiBiNET과 다른 점을 고려했을 때 bilinear function의 기능이 중요한 역할을 한다는 것을 볼 수 있었다고 합니다.
- FP-0과 FP-1을 비교하면 feature learning에서 feature importance를 고려하는 효과를 나타내며 정확한 feature embedding을 구축하는 것이 클릭률 예측 능력을 향상시킨다고 합니다.
- FP-12는 FP-0와 FP-1보다 더 좋은 성능을 보여주는데요. 이는 second order interaction encoder에서 어텐션 매커니즘의 중요성을 보여주는 것이고 feature learning에 필요한 관련있는 context들을 capture할 수 있는 것이라고 합니다. 게다가 모든 pair-wise feature interaction이 CTR 예측 task에서 동일하게 유용하지 않다는 것을 의미한다고 합니다.
- HAFP는 앞 세가지 변형 모델들과 비교하면 가장 좋은 성능을 보여주며 이는 hierarchical attention mechanism 구조가 본 모델에 기여한다는 것을 나타낸다고 합니다.
마무리
이번 포스팅은 추천 시스템의 클릭률 예측 논문인 Hierarchical attention and feature projection for click-through rate prediction 논문을 리뷰한 포스팅입니다. 해당 논문에 관심 있으신 분들에게 도움이 되시길 바랍니다.
감사합니다.




