이번 포스팅은 힙 정렬(heap sort)에 대해서 공부를 합니다.
먼저 힙(heap)에 대해서 알아야겠죠. 힙은 크기(우선 순위)을 중심으로 정렬된 시퀀스를 활용할 때 유용한 자료구조입니다. 힙은 한 노드가 최대 두 개의 자식노드를 가지면서 마지막 레벨을 제외한 모든 레벨에서 완전 이진트리(complete binary tree)를 기본으로 구조를 가지고 있습니다.
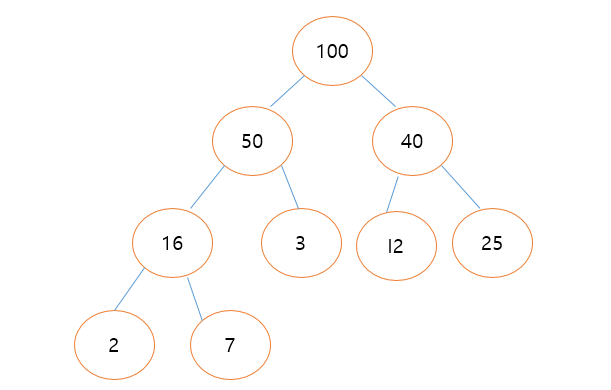
바로 위 사진처럼 되어 있는 구조가 힙 구조입니다. 잘 보면 이진 탐색 트리(binary search tree)와 구조가 살짝 차이가 있는데요
각 노드의 값은 자신의 자식노드보다 크거나 같습니다. 이게 이진 탐색 트리와는 차이점이죠. 이진 탐색 트리에서는 자식의 노드가 부모의 노드보다 값이 클 수도 있습니다. 하지만 힙에서는 그렇지 않습니다.
그리고 이것을 배열로 표현할 수 있는데요

이렇게 표현이 됩니다. 0번 인덱스(16)의 왼쪽 자식노드는 1번 인덱스(14)입니다. 2번 인덱스 자식노드는 4번 인덱스(9)입니다. 그러면 어떤 노드의 인덱스를 index라고 하고 왼쪽을 left_index, 오른쪽을 right_index라 하면
left_index = 2 * index + 1
right_index = 2 * index + 2
의 관계를 가집니다.
그리고 heapify라는 구조가 있습니다.
만약 데이터가 삽입, 삭제가 되면 힙의 성질(부모는 자식보다 크거나 같다)을 만족하는 방법이죠.
그래서 힙 정렬을 위해선 이 heapify 과정이 필요합니다.
힙 정렬은 아래와 같이 진행됩니다.
1. 정렬되지 않는 숫자들이 들어오면 bulid heap 합니다. build heap은 힙 구조가 만족되도록 힙을 만들어주는 것이죠(최대 힙)
2. 최대 힙 구조를 가지고 정렬을 진행
예를 들어서 list가 16, 9, 8, 14, 12, 10, 3 이라고 가정해보죠
그러면 아까 index를 구하는 공식 (left_index, right_index)를 이용해서 먼저 최대 힙 구조를 만들어주는 것입니다.

그러면 맨 처음은 위와 같은 구조로 되어 있을 겁니다.
이 상태에서 16과 9, 8을 봐야겠죠

9와 8은 16보다 작으므로 여기는 그냥 지나가도 됩니다.
즉 힙 구조가 되어 있죠
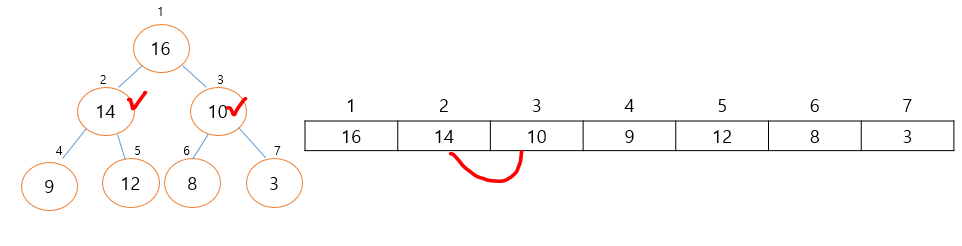
이와 같은 방식으로 아래를 보게 됩니다. 근데 여기서는 힙 구조가 성립이 되어 있지 않습니다.
일단 14가 9보다 크니까 옮겨줍니다. 근데 14는 9와 12보다 크므로 이제 성립됩니다.
그리고 8은 10보다 작습니다. 그래서 10이 위로 올라오게 됩니다. 이후 10은 8과 3보다 크므로 성립이 되서 끝이 납니다.
이렇게 힙 정렬이 수행이됩니다.
1. 최대힙 구성(0번 인덱스가 최댓값)
2. 최댓값을 배열 맨 마지막에 놓는다(큰 값을 뒤로)
3. 새로운 루트노드에 대해 최대힙 수행
4. 2~3 반복
이렇게 진행이 됩니다.
파이썬으로 코드를 구현하면 아래와 같습니다.
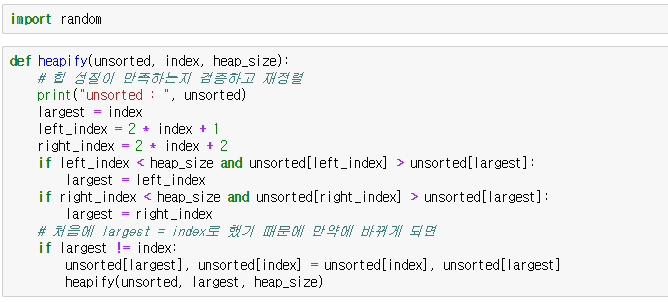
먼저 heapify입니다. 이것은 힙의 성질이 만족하는지 확인합니다.
만약 아래 노드가 위 노드보다 크면 그것을 바꿔줍니다. 그리고 재귀 호출하며 계속 반복합니다.

힙 정렬은 위와 같습니다. 먼저 시작하자마자 최대 힙을 구성해줍니다.
그리고 for i in range(n - 1, 0, -1): 부분에서
unsorted[0]과 unsorted[i] = unsorted[i], unsorted[0] 을 해주면서 리스트의 첫 번재 값과 마지막 값을 바꿔주고 다시 최대 힙을 구성하게 됩니다.
이렇게 되면 가장 큰 값이 맨 오른쪽으로 가게 됩니다!

위 사진은 맨 처음 최대 힙을 먼저 구성한 것입니다.
최대 힙을 구성하면 root에 가장 큰 값이 들어가죠

그리고 앞서 설명드린 것 처럼 최대 힙의 root 값이 말단 노드로 가게 되고 그 상태에서 다시 최대 힙을 구성합니다.
그리고 그 최대 힙을 구성하고 또 root와 말단을 바꿔주고 또 반복..
이것을 반복합니다.
그러면 정렬이 완료!

위와 같이 나오게 됩니다
'알고리즘&자료구조' 카테고리의 다른 글
| 파이썬 알고리즘 공부 - 최대공약수, 최소공배수 구하기 (4) | 2019.05.07 |
|---|---|
| 파이썬 알고리즘 공부 - 숫자 뒤집기(거꾸로 출력), 소수 출력, 배수 출력 (2) | 2019.04.29 |
| 합병정렬(merge sort) 혹은 병합정렬에 대해서 공부하자 - 파이썬 코드 (1) | 2019.04.23 |
| 파이썬으로 자료구조, 알고리즘 공부하기! 버블 정렬(bubble sort), 쉘 정렬(shell sort) (0) | 2019.04.23 |
| 파이썬으로 알고리즘, 자료구조 공부하기 - 삽입 정렬, 선택 정렬(selection sort, insertion sort) (1) | 2019.04.08 |




