포스팅 개요
해당 글에 대한 코드는 아래 github 링크에 전부 올려두었습니다.
lsjsj92/recommender_system_with_Python
recommender system tutorial with Python. Contribute to lsjsj92/recommender_system_with_Python development by creating an account on GitHub.
github.com
이번 포스팅은 파이썬(Python)으로 추천 시스템(Recommendation system) 기본을 구현해보는 포스팅입니다.
지난 포스팅에는 추천 시스템 협업 필터링(Collaborative Filtering)을 구현해봤습니다.
그 중 아이템 기반 협업 필터링(Item based Collaborative Filtering)을 구현했습니다.
https://lsjsj92.tistory.com/568
파이썬으로 추천 시스템(recommendation system) 구현해보기 - collaborative filtering
포스팅 개요 이번 포스팅은 파이썬(Python)으로 추천 시스템(recommendation system)을 개발해보는 포스팅입니다. 개발이라고 썼지만, 추천 시스템 개발이라기 보다는 공부하는 것이기 때문에 '구현'이라는 표현이..
lsjsj92.tistory.com
이번 포스팅은 이전 포스팅에 이어서 파이썬으로 추천 시스템 구현(Recommender system with Python)해보기 3탄으로 이어집니다.
그 중 협업 필터링을 구현할 것인데요. 지난 포스팅과 다르게 행렬 분해(Matrix Factorization)을 기반(잠재 요인 협업 필터링, latent factor collaborative filtering)으로 한 추천 시스템을 파이썬으로 구현해봅니다.
Python Recommendation System(Recommender system) : Collaborative Filtering Matrix Factorization
해당 자료는 아래에서 참고했습니다.
- https://www.kaggle.com/ibtesama/getting-started-with-a-movie-recommendation-system
- https://www.kaggle.com/rounakbanik/movie-recommender-systems
- https://github.com/SurhanZahid/Recommendation-System-Using-Matrix-Factorization/blob/master/Recommender%20System%20With%20Matrix%20Factorization%20.ipynb
- https://github.com/nikitaa30/Recommender-Systems/blob/master/matrix_factorisation_svd.py
데이터는 캐글의 MovieLens 데이터를 사용했습니다. (https://www.kaggle.com/sengzhaotoo/movielens-small)
포스팅 본문
협업 필터링(Collaborative Filtering) 요약
지난 포스팅에서 추천 시스템(Recommender System)의 협업 필터링(Collaborative Filtering)에는 크게 2가지 종류가 있다고 말씀드렸습니다.
- 아이템 기반 협업 필터링(Item based Collaborative Filtering) - nearest neighbor collaborative filtering
- 혹시 모르신다면 링크를 참고해주세요 (https://lsjsj92.tistory.com/563)
- 잠재 요인 기반 - SVD와 같은 행렬 분해(Matrix Factorization)를 사용
- 혹시 모르신다면 링크를 참고해주세요 (https://lsjsj92.tistory.com/564)
오늘 포스팅은 여기서 잠재 요인 기반 협업 필터링(Latent Factor Collaborative Filtering)을 파이썬(Python)으로 구현해봅니다.
파이썬 코드 구현
자! 이제 파이썬으로 추천 시스템을 구현해보죠
데이터는 앞서 개요에서 말씀드린 것처럼 Kaggle에 있는 movielens 데이터를 사용하겠습니다.
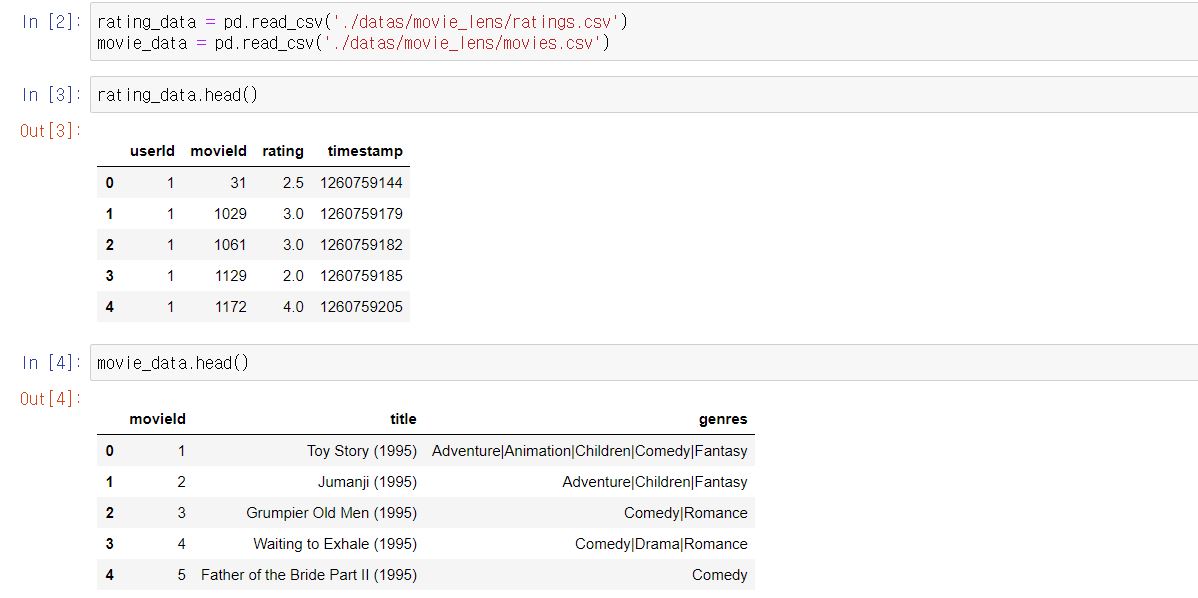
이 movielens 데이터는 2개로 나뉘어져 있는데요.
1. 사용자-영화 평점 기반 데이터
2. 영화 정보 데이터
영화 평점 데이터는 10만개가 넘고, 영화 데이터는 9000여개가 됩니다.

이렇게 말이죠!
이제 여기서 불필요한 데이터는 제거하고 필요한 데이터만 남기겠습니다.
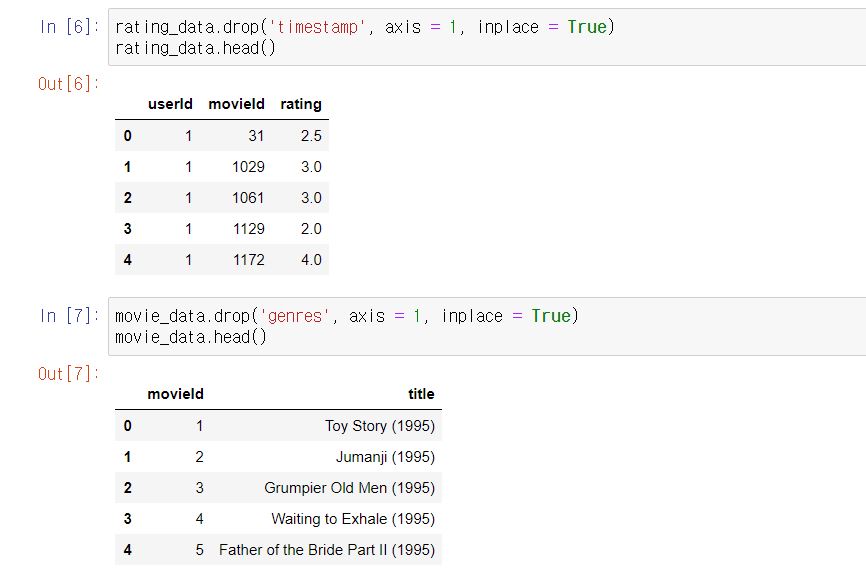
timestamp와 genres는 잠재 잠재요인 기반 협업 필터링 추천 시스템에서 필요없습니다.
따라서 drop을 이용해 두 컬럼을 각각 제거해줍니다.
자! 이제 2개의 파일을 pandas의 merge를 이용해서 합쳐줍니다.
2개의 데이터는 movieId라는 공통 컬럼이 있습니다. pd.merge(rating_data, movie_data, on = 'movieId')를 이용해 하나로 합쳐주겠습니다.
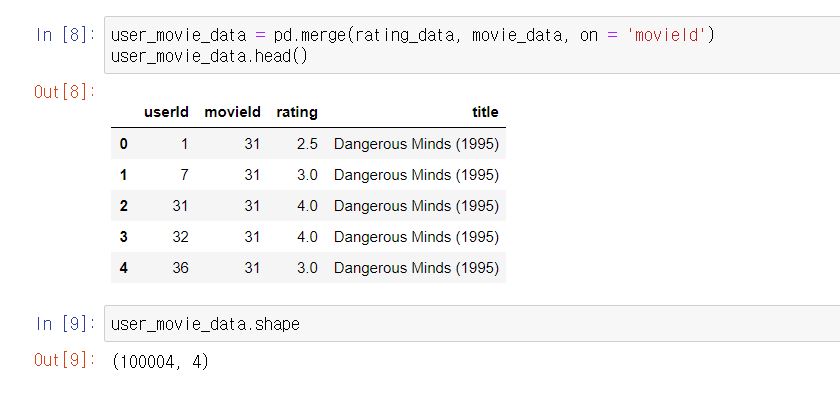
하나로 합쳤습니다! 그러면 특정 유저가 영화에 대해 평점을 매겼는데 그 영화의 제목(title)이 무엇인지 알 수 있게 되었습니다.
자! 이제 pandas의 pivot table을 이용해서 데이터를 변경시켜주어야 합니다.
지금은 user, movie, rating이 각각 컬럼에 존재하는데요. 이렇게 생긴 데이터를 value를 평점으로 column은 movie로, row는 user id로 바꿔주어야 합니다. 아래 그림처럼요!
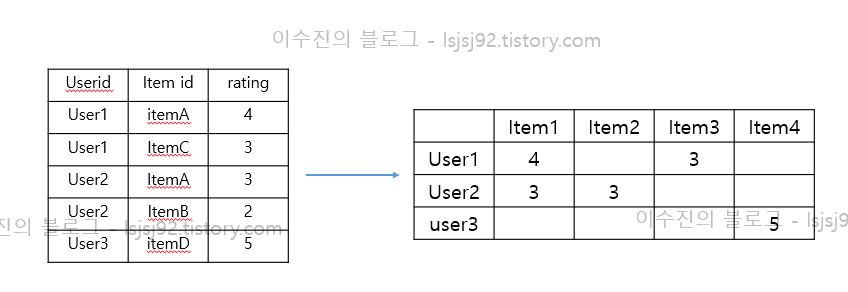
이렇게 변환하는 것을 pandas에서 pivot_table이라는 것으로 지원해줍니다.
바꿔주죠!
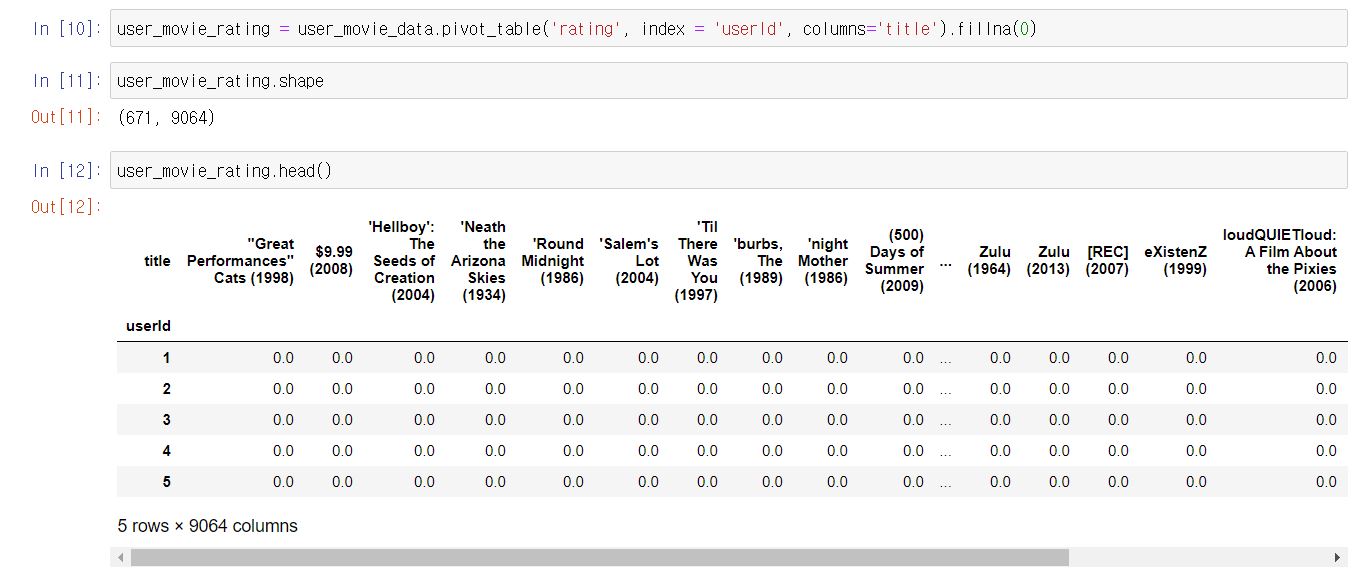
user_movie_data.pivot_table('rating', index = 'userId', columns='title')로 바꿔주면 사용자-영화 평점 데이터로 변경해줍니다.
단, 단순히 저렇게만 하면 사용자가 평점을 매기지 않은 정보에는 NaN값이 들어가니 fillna을 사용해 0으로 채워줍시다.
이제 이 데이터를 어떻게 활용할까? 이것을 고민해야 하는데요.
이번 포스팅에서는 '특정 영화와 비슷한 영화를 추천' 해주는 컨셉으로 가볼까합니다.
그래서 현재 user-movie로 되어 있는 pivot table을 movie-user data로 바꿔줍시다.
numpy에서 .T를 사용하면 Transpose를 시켜줍니다. 즉, 전치를 시켜줍니다.
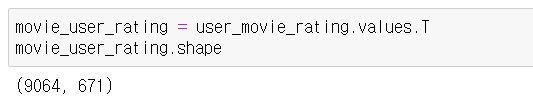
이렇게 전치로 바꿔주면 행은 9064개의 영화 데이터가 되고 열은 671개의 사용자 데이터가 됩니다.
이제 SVD라는 개념을 적용해서 사용해봅니다.
SVD(Singular Value Decomposition)란?
SVD라는 것은 특이값 분해라고도 불리웁니다. M x N 크기의 데이터 행렬 A를 아래와 같이 분해합니다.
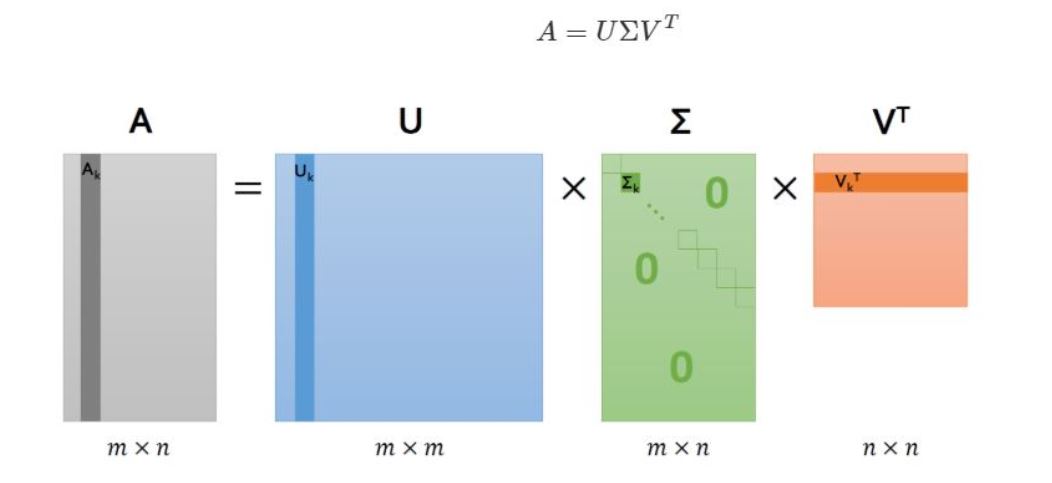
제가 많이 참조하고 배우고 있는 ratsgo님의 블로그에 자세히 설명이 쓰어져 있는데요.
간단히 말하면 SVD는 다음과 같습니다.
행렬 U와 V에 속한 열벡터는 특이 벡터(Singular Vector)라 불리고 이 특이 벡터들은 서로 직교하는 성질을 가지고 있습니다.
또한 가운데 시그마 모양(∑)을 가지고 있는 것도 행렬인데요.
이 행렬은 대각 행렬(Diagonal Matrix) 성질을 가지고 있습니다.
그래서 대각 성분이 행렬 A의 특이값이고 나머지는 0의 값을 가지고 있습니다.
저렇게 특이값으로 쪼개진 데이터를 U, ∑, Vt를 각각 행렬곱을 하면 원래 행렬 A로 되돌릴 수 있습니다.
파이썬 사이킷런(Python scikit learn)에서 제공해주는 TruncateSVD는 이러한 SVD의 변형입니다.
TruncatedSVD는 시그마 행렬(∑)의 대각원소(특이값) 가운데 상위 n개만 골라낸 것입니다.
이렇게 하면 기존 행렬 A의 성질을 100% 원복할 수 없지만 (그 만큼 데이터 정보를 압축했기 때문)
행렬 A와 거의 근사한 값이 나오게 됩니다.
여기서는 scikit learn의 TruncatedSVD를 사용합니다.
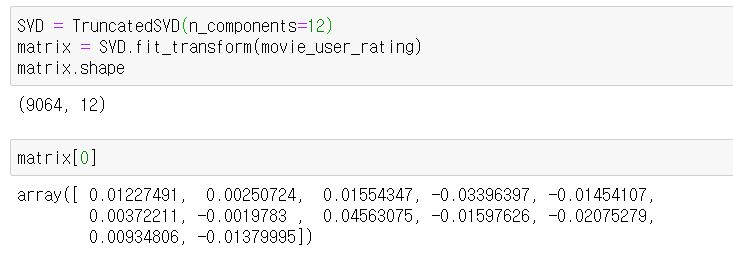
scikit learn의 TruncatedSVD를 사용하고 안에 latent 값을 12로 두겠습니다.
그리고 SVD.fit_transform을 통해 변환을 하게 되면 9064개의 영화 데이터가 12개의 어떤 요소의 값을 가지게 됩니다.
이렇게 나온 데이터끼리 피어슨 상관계수를 통해 구해줍니다.

numpy에 있는 corrcoef를 이용하면 상관계쑤를 구할 수 있도록 해줍니다
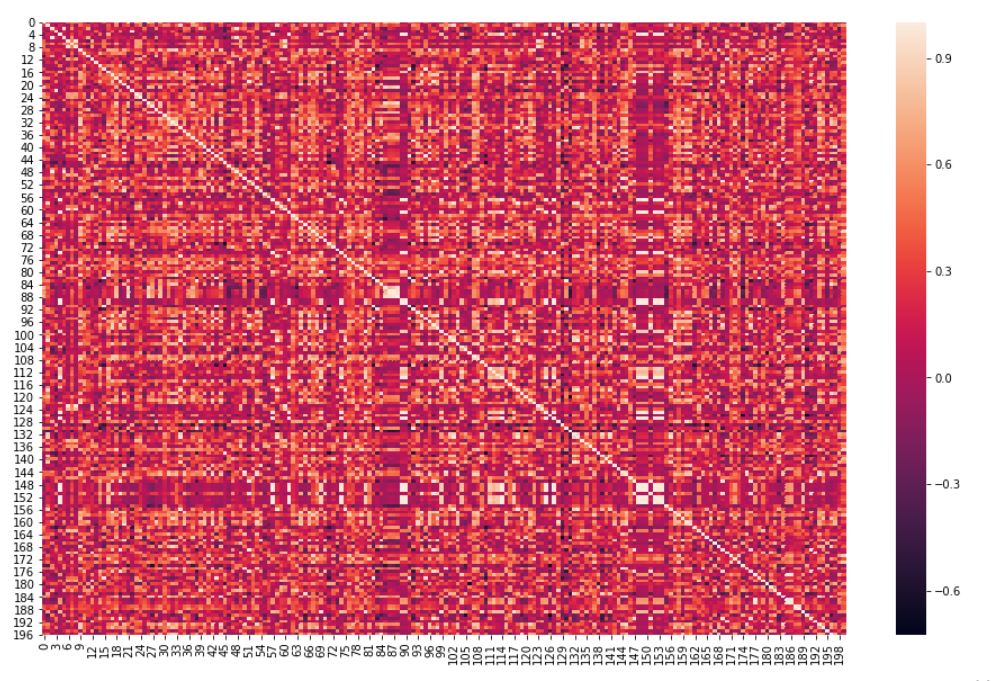
seaborn의 heatmap을 사용하면 이 상관계수끼리의 관계를 볼 수 있습니다.
대각선이 하얀색인 이유는 자기 자신과의 관계니까 가장 높은 하얀색이 나온 것입니다.
이렇게 나온 상관계수를 이용해서 '특정 영화'와 관련하여 상관계수가 높은 영화를 뽑아주면 됩니다.
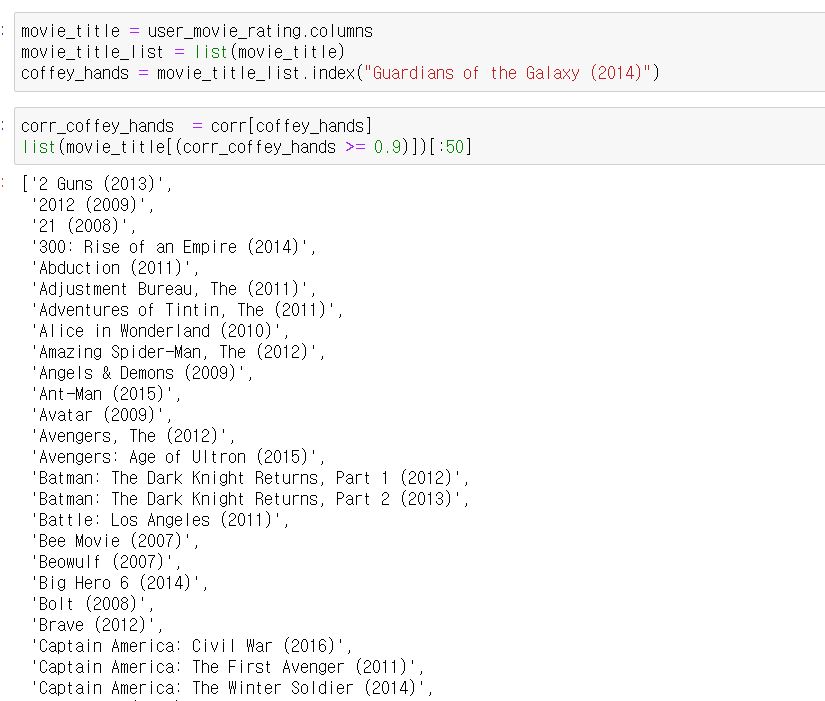
마블의 가디언즈 오브 갤럭시를 지정하여 상관계수가 높은 영화를 뽑아봤는데요.
영화 목록은 아래와 같습니다.
- 영화 투 건즈
- 영화 2012
- 영화 300
- 마블 엔트맨
- 마블 어벤져스
- 베트맨
등등의 영화가 마블의 가디언즈 오브 갤럭시와 비슷하다고 추천되었습니다!
뭔가 그럴듯한 결과가 나왔네요!
이번 포스팅에서는 파이썬을 활용해 추천 시스템을 구현해보았습니다.
이번 추천 시스템 구현은 잠재 요인 협업 필터링(latent factor collaborative filtering)에 대해서 구현했고 이를 위해 행렬 분해(matrix factorization)을 사용했습니다. 행렬 분해를 위해서 SVD를 사용했구요.
이번 포스팅은 '특정 영화'와 비슷한 영화 들을 추천해주었습니다.
마치 아이템 기반 협업 필터링과 비슷했죠?
이것은 사용자가 본 history를 생각하지 않은 결과입니다. 즉, 사용자에게 추천하기에는 부족하죠.
따라서 다음 포스팅에서는 사용자 맞춤 개인 추천 시스템을 구현하는 포스팅을 작성하겠습니다.
저에게 연락을 주시고 싶으신 것이 있으시다면
- Linkedin : https://www.linkedin.com/in/lsjsj92/
- github : https://github.com/lsjsj92
- 블로그 댓글 또는 방명록
으로 연락주시면 감사하겠습니다.
'추천시스템' 카테고리의 다른 글
| Keras를 활용한 딥러닝 추천 시스템(deep learning recommender system) 구현하기 (30) | 2020.03.08 |
|---|---|
| 파이썬(Python)으로 간단한 뉴스 추천 시스템(recommender system) 구현해보기 (22) | 2020.02.04 |
| 파이썬 Matrix Factorization 영화 추천 시스템(movie recommender system) 구현해보기 - 2 (55) | 2020.01.31 |
| 파이썬으로 추천 시스템(recommendation system) 구현해보기 - collaborative filtering (18) | 2020.01.19 |
| 파이썬과 함께 추천 시스템(recommendation system) 이해하기 기본편 - content based filtering (15) | 2020.01.08 |





